Sommaire
- 1. La courbe en cloche (Gaussienne)
- 2. Comparaison de deux courbes en cloche
- Références
- Liens
- Historique des modifications
1. La courbe en cloche (Gaussienne)
La "courbe en cloche" ("Bell Curve") est la courbe la plus célèbre des statistiques, et à raison. Si elle est souvent associée à la distribution des QI au sein d'une population, elle est beaucoup plus que cela : elle décrit la distribution que l'on retrouve généralement quand celle-ci dépend de suffisamment d'éléments suffisamment indépendants entre eux. Les exemples sont innombrables : la taille, le poids, la précision d'un tir, etc., etc. Tout ne suit pas une Loi Normale (!) mais on la retrouve souvent.
1.1 Définition
Au niveau mathématique elle représente graphiquement une distribution suivant une Loi Normale dont le premier avantage est d'être très simple : pour la définir, il suffit de connaître sa Moyenne et son Écart-Type :
- La Moyenne ("M", ou "µ" qui se lit "Mu") est la somme de toutes les valeurs divisée par leur nombre ("Moyenne arithmétique").
Dans une distribution suivant une Loi Normale, la Moyenne est aussi la Médiane (valeur centrale : autant d'éléments d'un côté et de l'autre) et son Mode (valeur la plus représentée). - L'Écart-Type ("σ" qui se lit "sigma", ou "SD" pour "Standard Deviation") est la racine carrée de la Variance, laquelle est la moyenne arithmétique des carrés des écarts à la moyenne.
L'Écart-Type quantifie la dispersion : plus il est élevé relativement à la moyenne, plus la courbe apparaît aplatie, et donc moins la moyenne décrit la population sur le critère étudié. Cela est mesuré par le Coefficient de variation qui correspond tout simplement au ratio Écart-Type/Moyenne (souvent exprimé en pourcentage).
On notera que dans les études scientifiques l'écart-type est généralement indiqué par le signe±(exemple : "27±8" signifie : M=27, σ=8).
1.2 Exemple
Imaginez que vous cherchiez la taille moyenne d'une classe. Vous mesurez chacun des 24 élèves et trouvez que 2 font moins de 1,60 m, 5 font entre 1,60 et 1,70 m, 10 font entre 1,70m et 1,80m, 5 font entre 1,80m et 1,90m, et 2 plus de 1m90. Votre méthode n'est pas très précise, aussi vous décidez de considérer que chaque segment de taille est représenté par sa moitié : 1,55m pour moins de 1,60m, puis 1,65m, 1,75m, 1,85m, et enfin 1,95m :
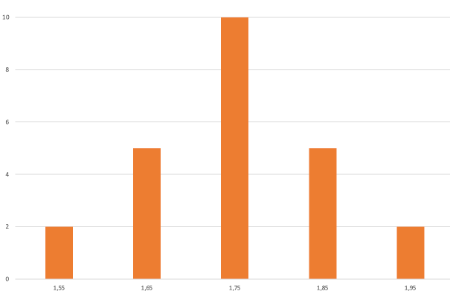
La taille moyenne (en m) peut dès lors être calculée : [(2 x 1,55) + (5 x 1,65) + (10 x 1,75) + (5 x 1,85) + (2 x 1,95)] / 24 = 1,75
C'est la valeur que vous souhaitiez calculer, mais elle est fortement limitée : avec ce seul chiffre de 1,75 m vous ne pouvez pas savoir combien sont loin de cette valeur, ils pourraient être tous entre 1,70 m et 1,80 m. Il vous faut pour le savoir calculer l'Écart-Type, c'est-à-dire :
- Calculer les écarts à la moyenne pour chaque valeur :
(1,55 - 1,75) = -0,2;(1,65 - 1,75) = -0,1;(1,75 - 1,75) = 0;(1,85 - 1,75) = 0,1;(1,95 - 1,75) = 0,2 - Les mettre au carré :
(-0,2)² = 0,04;(-0,1)² = 0,01;(0)² = 0;(0,1)² = 0,01;(0,2)² = 0,04 - Les pondérer avec le nombre d'élèves pour chaque :
0,04 x 2 = 0,08;0,01 x 5 = 0,05;0 x 10 = 0;0,01 x 5 = 0,05;0,04 x 2 = 0,08 - Diviser le total obtenu par le nombre d'élèves (c'est la moyenne) pour obtenir la Variance :
0,26 / 24 ≈ 0,011 - L'Écart-Type est la racine carrée de cette Variance :
√0,011 ≈ 0,10
Et le Coefficient de variation (ratio Écart-Type/Moyenne) est : 0,10 / 1,75 ≈ 5,7%
Si la distribution étudiée suivait une Loi Normale (ce qui n'est pas le cas de notre exemple !) alors on pourrait en déduire combien de personnes sont à chaque valeur.
1.3 Loi Normale Centrée Réduite et Z Score
Si vous savez que dans une distribution suivant une Loi Normale de Moyenne 100 et d'Écart-Type 15 (comme le QI Standard) un élément se situe à 115, vous savez qu'il est à exactement +1σ de la Moyenne : exactement comme s'il se situait à 1 dans une distribution suivant une Loi Normale de Moyenne 0 et d'Écart-Type 1.
De fait, vous pouvez très facilement convertir toute Loi Normale ayant ses propres Moyenne et Écart-Type en une Loi Normale Centrée Réduite se caractérisant par une Moyenne égale à 0 et un Écart-Type égal à 1.
Cela revient à compter en Écart-Types (pour obtenir un "Z Score"), avec l'avantage que vous pouvez maintenant vous référer à des tables qui vous indiqueront précisément les pourcentages de la population compris entre chaque écart-type :
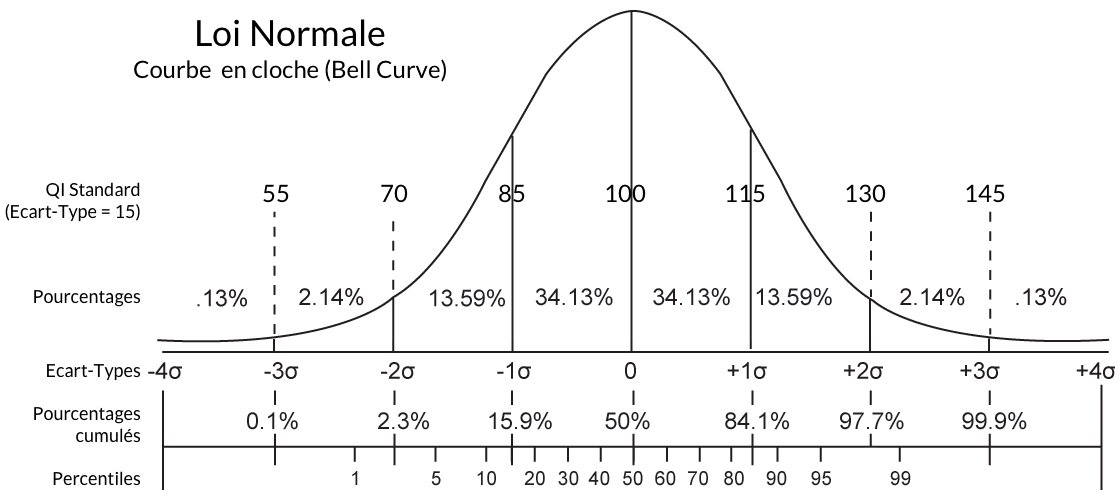
En fait, avec une table suffisamment précise (ex : la z table disponible en ligne donne les résultats au centième), on peut même repartir du pourcentage de la population pour retrouver le Z score, c'est-à-dire la valeur correspondante en écart-types dans une distribution suivant une Loi Normale.
Il faut cependant se rappeler que cette conversion fait perdre le lien avec la réalité physique mesurée :
- Elle fait perdre l'importance de la moyenne
- Elle fait perdre l'information sur la taille relative de l'écart-type (le Coefficient de Variation), et donc à quel point la population est dispersée sur le critère mesuré
1.4 T Score
Le nom T Score a trois significations, dont une en lien direct avec la Loi Normale :
En Psychométrie, le T Score correspond à une Loi Normale de Moyenne 50 et d'écart-type 10 (ex : 20 = -3σ, 60 = +1σ, etc.) et est donc une autre manière de présenter une Loi Normale Centrée Réduite avec l'avantage de ne pas avoir de valeur négative.
En statistiques, le T Score correspond à la valeur obtenue par une Loi de Student, qui est une loi statistique adaptée aux petits échantillons quand la Variance de la population totale est inconnue. Elle converge vers la Loi Normale Centrée Réduite quand le nombre de valeurs augmente. Ce T Score peut avoir des valeurs négatives.
En médecine, le T Score est la mesure suivant une Loi Normale Centrée Réduite (µ=0, σ=1) de la densité osseuse par rapport à la population d'adultes en bonne santé âgés de 30 ans.
1.5 Conséquences
Il est important de remarquer que la courbe descend très vite :
- Plus des deux tiers (68,2%) de la population est entre -1 et +1 écart-type, moins du tiers (< 1/3) est en dehors : il y a plus de deux fois plus de chances d'être dans cette zone centrale qu'en dehors.
- Seulement 1/50 est à +2σ (en QI standard : 130)
- Seulement 1/1 000 est à +3σ (en QI standard : 145)
- Seulement 1/31 000 est à +4σ (en QI standard : 160)
-...
Pour illustrer les proportions, cette grille montre dans une population de 1 000 cases d'un côté la la proportion de -1σ (vert + bleu ciel + bleu), -2σ (bleu ciel + bleu), et -3σ (bleu) et de l'autre la proportion de +1σ (vert + bleu ciel + bleu), +2σ (bleu ciel + bleu), et +3σ (bleu), les cases blanches montrant la proportion comprise entre -1σ et +1σ :
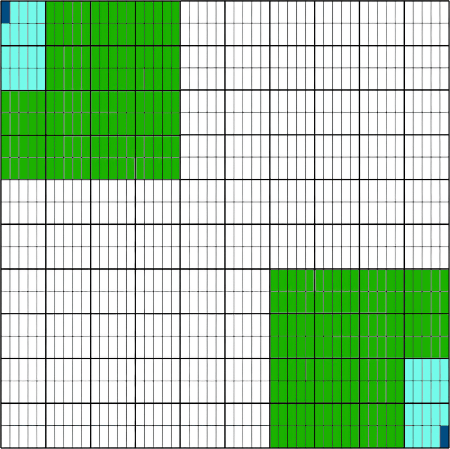
On remarque que les +4σ ne peuvent pas être représentés sur cette image : leur proportion correspond à moins de 1/31e de case, soit à cette échelle moins qu'un pixel...
1.5.1 Normalité
La première conséquence est que nous sommes sur de nombreux critères entre -1σ et +1σ (la partie blanche sur le graphique ci-dessus).
C'est ce qu'avait expliqué la Base Éco 17 :
"Dès lors nous pouvons définir ce qu’est la normalité : c’est être dans la norme, c’est-à-dire à moins d’un écart-type de la moyenne sur un critère suivant la Loi Normale dans une population définie. En d’autres termes : 68,2% de cette population est normale sur ce critère.
Au sein de la population humaine, nous sommes tous normaux sur la plupart des critères qui nous définissent (taille, poids, santé, etc.) dans notre groupe usuel. Mais le simple fait d’être anormaux (à plus de 1 écart-type de la moyenne) sur quelques autres suffit à nous rendre, tous, uniques. C’est cette opposition qui explique pourquoi il est beaucoup plus facile de manipuler les foules, que ce soit pour des objectifs commerciaux ou politiques, qu’un individu unique : c’est elle qui fonde tout le marketing.
La normalité n’a rien à voir avec la moralité, elle n’est qu’une caractéristique statistique."
Base Éco 17 : Qu’est-ce qu’être normal ?
1.5.2 Rareté
Une autre conséquence est que les extrêmes sont (très !) rares : si tout le monde autour de vous se vante d'être THQI (QI ≥ 145 : +3σ soit 1,3/1 000), soit vous êtes dans un club dédié, soit certains mentent...
1.5.3 Non-représentativité
Et une conséquence de cette conséquence est que les études sur les +2σ ne nous disent rien sur les +3σ et +4σ :
- Seulement 1/20 d'un échantillon de +2σ est à +3σ
- Seulement 1/717 d'un échantillon de +2σ est à +4σ
Et c'est encore pire avec les études sur les top 5% (+1,67σ)...
1.5.4 Intervalle de confiance
Mais à l'opposé on peut se servir de cette centralisation des valeurs pour calculer l'intervalle de confiance qui correspond au pourcentage voulu de la population : on peut connaître les valeurs définissant un intervalle tel que si on prend un composant au hasard de cette population, on a le pourcentage voulu de chances qu'il soit dans cet intervalle de confiance et le pourcentage voulu de chances qu'il n'y soit pas.
Comme la courbe en cloche est symétrique, et qu'on connait grâce à la Loi Normale Réduite les pourcentages à chaque niveau d'écart-type, il suffit de se reporter à la z table pour trouver l'intervalle de confiance.
Par exemple si on veut caculer un intervalle de confiance à 95% pour une distribution suivant une Loi Normale de moyenne M=100 et d'écart-type σ=15:
- 95% correspond à l'intervalle compris entre 2,5% et 97,5% de la population
- Dans la z table nous trouvons que 2,5% (0,025) correspond à -1,96 écart-types (ligne : -1,9 ; colonne : 0,06), juste un peu moins que -2σ.
- Comme la distribution est symétrique, l'intervalle de confiance est donc compris entre -1,96σ et +1,96σ
- On multiplie cette valeur par l'écart-type et on crée l'intervalle à partir de la moyenne :
- Borne inférieure : 100 - (1,96 x 15) = 70,6
- Borne supérieure : 100 + (1,96 x 15) = 129,4
Donc, dans cette population (M=100, σ=15), 95% de la population est entre 70,6 et 129,4.
Pour un intervalle de confiance de 99%, on obtient ±2,58σ (soit dans la même population avec M=100 et σ=15 : entre 61,3 et 138,7), et pour un intervalle de confiance de 90% on obtient ±1,28σ (entre 80,8 et 119,2).
1.5.5 L'erreur NAXALT
Une erreur fréquente s'appelle la NAXALT fallacy ("Not all X are Like That" : "Tous les X ne sont pas comme ça"), c'est-à-dire la croyance erronée que parce qu'il existe des extrêmes la moyenne n'existe pas :

Par exemple, la réponse "Il y a des femmes qui font 1m90" pour contester l'affirmation que les femmes sont plus petites que les hommes est une NAXALT.
La NAXALT est énormément utilisée en propagande politique : un exemple totalement hors norme est présenté comme réfutant une constatation générale.
2. Comparaison de deux courbes en cloche

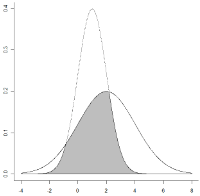
Jusqu'ici, nous n'avons étudié qu'une seule population. Il est parfois intéressant de s'intéresser aux composantes de cette population, afin de voir si des différences de groupes apparaissent. C'est quelque chose de très fréquent, par exemple les études de taille distingueront généralement les deux sexes, les femmes étant en moyenne (voir ci-après) plus petites que les hommes (image ci-dessus).
Une distribution suivant une Loi Normale étant définie par sa Moyenne et son Écart-Type, il faut dès lors comparer ces distribution sur ces deux valeurs, le cas le plus simple étant celui ou les Écart-types sont identiques. L'objectif premier est de déterminer à quel point ces courbes se chevauchent, quels sont les ratios aux extrêmes, et si les différences sont suffisamment importantes pour que leur effet se remarque au niveau de la population globale (courbe à une ou deux bosse(s)).
2.1 Chevauchement
Il est rare de tomber sur des courbes qui ne se chevauchent pas : il faut pour cela que la différence de moyenne soit très importante relativement aux écarts-types. Le plus souvent il y a chevauchement (anglais : "Overlap") : les femmes sont en moyenne plus petite que les hommes mais certaines sont plus grandes que certains hommes, etc.
Il est mesuré par le Coefficient de chevauchement ("Overlap coefficient") qui existe sous différentes formes, et son calcul peut-être compliqué, notamment quand les écart-types sont très différents comme dans l'image ci-dessus (source). On trouve en ligne des aides, comme ce graphique (Rash) :
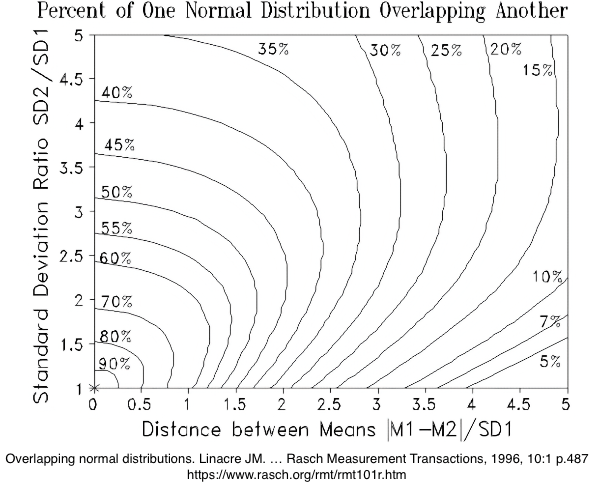
"Si M1=2,4, SD1=1,6, et M2=3,2, SD2=2,0, alors | M2-M1 | /SD1=0,5, SD2/SD1=1,25, et, en référence au nomogramme, environ 80% de chaque distribution recouvre l'autre."
Rash (1996)1
Le point à retenir est que le plus souvent connaître la valeur d'une personne sur un critère ne suffit pas à déterminer à quelle sous-population appartient cette personne, mais n'en donne qu'une probabilité (un exemple en avait été donné Base Éco 12).
2.2 Différence aux extrêmes
Cette limite n'implique pas que la différence entre deux distributions serait à négliger : plus on s'éloigne de la moyenne, plus la différence est importante.
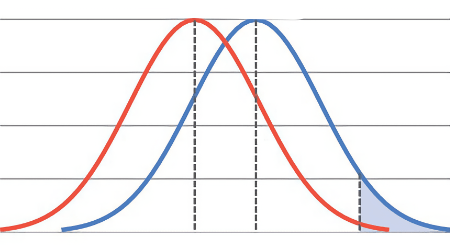
Par exemple, si deux distributions montrant le même écart-type ont leurs moyennes éloignées de 1σ et sont rassemblées :
- Seulement 16% de la première distribution atteint le niveau moyen de la seconde
- Seulement 2% de la première distribution atteint le niveau +1σ de la seconde
- Seulement 0,1% de la première distribution atteint le niveau +2σ de la seconde
-...
Soit, si 1 000 personnes d'une population A au QI Standard moyen de 100 et 1 000 personnes d'une population B au QI Standard moyen de 115 sont rassemblées, on trouve au-dessus de chaque niveau :
| QI | 100 | 115 | 130 | 145 | 160 |
|---|---|---|---|---|---|
| Population A (QI moyen 100) | 500 | 160 | 23 | 1 | 0 |
| Population B (QI moyen 115) | 660 | 500 | 160 | 23 | 1 |
| Total | 1 160 | 660 | 183 | 24 | 1 |
| Pourcentage provenant de la Pop. A | 43% | 24% | 12% | 4% | 0% |
| Pourcentage provenant de la Pop. B | 57% | 76% | 88% | 96% | 100% |
2.3 Courbes bimodales
Une autre manière de voir les choses est de se demander à quoi ressemble la courbe de l'union de deux sous-populations :
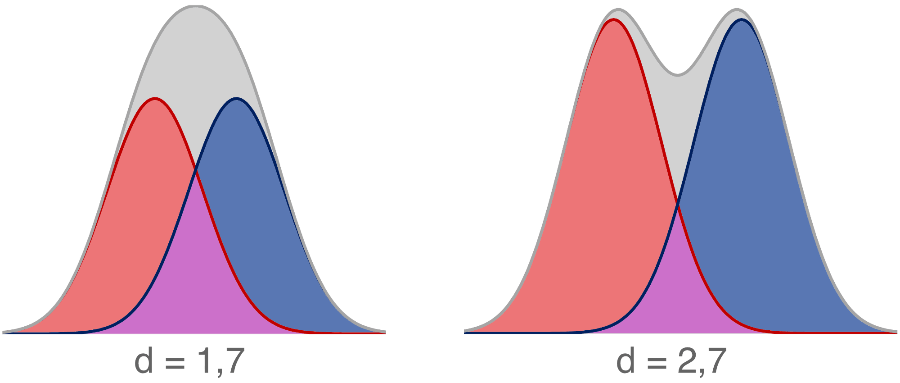
"Comme indiqué dans la Base Éco 12, on peut aussi s’intéresser à l’addition de plusieurs courbes en cloches. Par exemple on peut vouloir comparer la distribution selon le sexe ou selon l’âge. Est-ce que l’addition de deux courbes donne aussi une courbe en cloche ? En d’autres termes : une courbe en cloche peut-elle être l’addition de deux ou plusieurs courbes en cloche ? En fait oui, souvent : il faut que l’écart entre les moyennes soit supérieur à deux écarts-types pour qu’une addition montre une courbe à deux bosses (Schilling et al. 2002). Pourtant, ce niveau d’écart est déjà énorme : seulement 2,3% d’une des sous-populations dépasse le niveau moyen de l’autre."
Base Éco 17 : Qu’est-ce qu’être normal ?
A noter que selon Schilling et al. 2002 la différence sexuelle de taille aux USA n'est que de 1,7σ (courbe de gauche sur le graphique ci-dessus), ce qui signifie que la courbe globale rassemblant les deux sexes est unimodale (et que la photo ci-dessus d'étudiants américains n'est pas représentative).
2.4 Pertinence
Cela signifie directement que le simple fait qu'il y ait une différence de moyenne sur un critère entre deux populations ne suffit pas à les distinguer l'une de l'autre, ce qui implique :
Décider à partir de quel niveau de distance en écart-types deux populations peuvent être considérées comme différentes sur un critère est un choix qui doit être fait en fonction de la pertinence de cette distinction. Voir : Races, Racisme et Evopsy sur Evoweb.
Une caractéristique ne fait pas une identité ! Voir : Qu'est-ce qu'une femme ? sur Evopsy.
En revanche, il faut aussi se rappeler que même un petit écart de moyenne provoque des différences très importantes aux extrêmes sur le critère étudié.
2.5 Les chiffres
2.5.1 Visualisation
Kristoffer Magnusson a mis en ligne une magnifique visualisation interactive de la comparaison de deux courbes en cloche : Interpreting Cohen's d Effect Size - An Interactive Visualization. Il suffit d'y faire glisser un slider pour obtenir à la fois une visualisation (comme celle-ci après) et les principaux chiffres correspondants.
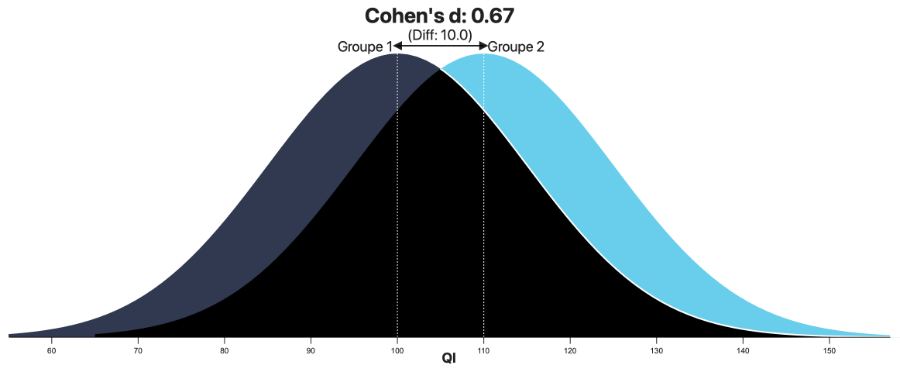
En utilisant l'outil de Kristoffer Magnusson on obtient :
| Écart en QI | Écart en d | U3 de Cohen2 | Chevauchement | Probabilité de supériorité CL3 |
|---|---|---|---|---|
| 1 | 0,07 | 52,7% | 97,3% | 51,9% |
| 5 | 0,33 | 63,0% | 86,8% | 59,3% |
| 7,5 | 0,50 | 69,1% | 80,3% | 63,8% |
| 10 | 0,67 | 74,9% | 73,8% | 68,2% |
| 15 | 1,00 | 84,1% | 61,7% | 76,0% |
| 20 | 1,33 | 90,8% | 50,6% | 82,7% |
| 25 | 1,67 | 95,2% | 40,5% | 88,1% |
| 30 | 2,00 | 97,7% | 31,7% | 92,1% |
Lecture : Un écart de moyenne de 10 points de QI pour un écart-type de 15 dans les deux groupes (image ci-dessus) corespond à un d de Cohen de 0,67 (2/3) ; 74,9% du Groupe 2 a un QI supérieur à 50% du Groupe 1 ; si vous prenez une personne au hasard, dans 73,8% des cas vous ne pourrez déterminer à quel groupe elle appartient ; mais si vous prenez au hasard une personne dans chaque groupe, il y a 68,2% de chances que celle du Groupe 2 ait un QI supérieur.
2.5.2 Tableau MS Excel
Stat-Help.com propose au téléchargement un tableau MS Excel pour calculer U1, U2, U3, BESD, et CL : Statistics to interpret d.
Le tableau suivant a été généré avec cet outil en augmentant le d de Cohen de 0,166666, soit 2,5 points de QI standard, à chaque ligne (le fichier MS Excel calcule à 15 chiffres après la virgule) :
| Δ QI | d | U1 | U2 | U3 | BESD | CL |
|---|---|---|---|---|---|---|
| 2,50 | 0,17 | 0,12 | 0,53 | 0,57 | 0,07 | 0,55 |
| 5,00 | 0,33 | 0,23 | 0,57 | 0,63 | 0,13 | 0,59 |
| 7,50 | 0,50 | 0,33 | 0,60 | 0,69 | 0,20 | 0,64 |
| 10,00 | 0,67 | 0,41 | 0,63 | 0,75 | 0,26 | 0,68 |
| 12,50 | 0,83 | 0,49 | 0,66 | 0,80 | 0,32 | 0,72 |
| 15,00 | 1,00 | 0,55 | 0,69 | 0,84 | 0,38 | 0,76 |
| 17,50 | 1,17 | 0,61 | 0,72 | 0,88 | 0,44 | 0,80 |
| 20,00 | 1,33 | 0,66 | 0,75 | 0,91 | 0,50 | 0,83 |
| 22,50 | 1,50 | 0,71 | 0,77 | 0,93 | 0,55 | 0,86 |
| 25,00 | 1,67 | 0,75 | 0,80 | 0,95 | 0,60 | 0,88 |
| 27,50 | 1,83 | 0,78 | 0,82 | 0,97 | 0,64 | 0,90 |
| 30,00 | 2,00 | 0,81 | 0,84 | 0,98 | 0,68 | 0,92 |
| 32,50 | 2,17 | 0,84 | 0,86 | 0,98 | 0,72 | 0,94 |
| 35,00 | 2,33 | 0,86 | 0,88 | 0,99 | 0,76 | 0,95 |
| 37,50 | 2,50 | 0,88 | 0,89 | 0,99 | 0,79 | 0,96 |
| 40,00 | 2,67 | 0,90 | 0,91 | 1,00 | 0,82 | 0,97 |
| 42,50 | 2,83 | 0,92 | 0,92 | 1,00 | 0,84 | 0,98 |
| 45,00 | 3,00 | 0,93 | 0,93 | 1,00 | 0,87 | 0,98 |
| 47,50 | 3,17 | 0,94 | 0,94 | 1,00 | 0,89 | 0,99 |
| 50,00 | 3,33 | 0,95 | 0,95 | 1,00 | 0,90 | 0,99 |
| 52,50 | 3,50 | 0,96 | 0,96 | 1,00 | 0,92 | 0,99 |
Références
Krings, M., Stone, A., Schmitz, R. W., Krainitzki, H., Stoneking, M., & Pääbo, S. (1997). Neandertal DNA Sequences and the Origin of Modern Humans. Cell, 90(1), 19–30 doi:10.1016/S0092-8674(00)80310-4
Schilling, M. F., Watkins, A. E., & Watkins, W. (2002). Is Human Height Bimodal? The American Statistician, 56(3), 223–229 doi:10.1198/00031300265
Liens
-
- Base Éco 12 : Bayes et le grand nombre. Philippe Gouillou. Monaco Business News 76. 30 octobre 2021
- Base Éco 17 : Qu’est-ce qu’être normal ?. Philippe Gouillou. Monaco Business News 78. 29 avril 2022
Douance :
- Table de conversion du QI (Wechsler <-> Catell). Philippe Gouillou. Douance. 1999 - Mise à jour : 24 novembre 2011
- Répartitions théoriques du QI en fonction du QI moyen de la population : Table donnant le pourcentage de personnes ayant un QI standard à plus ou moins un ou deux écart-type(s) d'un QI donné, en fonction de la population
- Le QI de la partie droite de la courbe : Quel est le QI moyen d'une population qui ne comprend que les personnes ayant un QI supérieur à une valeur ?
- QI auto-estimé vs QI réel. Philippe Gouillou. Douance. 7 avril 2020
Qu'est-ce qu'une femme ?. Philippe Gouillou. Evopsy. 31 Décembre 2022 - MàJ : 10 janvier 2023
Races, Racisme et Evopsy. Gouillou, Philippe. Evoweb. 12 octobre 2004
Rash (1996). Overlapping Normal Distributions. John M. Linacre
Stat-Help.com : Microsoft Excel Spreadsheets.
Historique des modifications
| Date | Historique |
|---|---|
| 19 janvier 2024 | Ajout tableau à 2.2 Différence aux extrêmes |
| 19 octobre 2024 | Ajout 1.5.5 L'erreur NAXALT |
| 1 mai 2024 | Ajout 1.4 T Score et renumérotation (1.4 → 1.5) |
| 5 Février 2024 | Ajout 2.5 Les chiffres |
| 7 Février 2023 | Complément à 2.4 Pertinence |
| 6 Février 2023 | Orthographe |
| 1 Février 2023 | Ajout 1.4.4 Intervalle de confiance |
| 29 Janvier 2023 | 1ère Mise en ligne |
Notes
-
Traduction depuis :
If M1=2.4, SD1=1.6, and M2=3.2, SD2=2.0, then | M2-M1 | /SD1=0.5, SD2/SD1=1.25, and, by reference to the nomogram, about 80% of each distribution overlaps the other.
Rash (1996) -
U3 de Cohen : proportion du groupe 2 ayant un score supérieur à la moyenne du groupe 1.
La formule pour le calculer sous MS Excel est :LOI.NORMALE.STANDARD(d de Cohen)↩ -
La Probablité de supériorité est le "Common Language effect size statistic (CL)" de McGraw & Wong (1992, doi:10.1037/0033-2909.111.2.361).
Il est calculé en divisant la différence entre les deux moyennes par la racine carrée de la somme de leurs variances, puis en déterminant la probabilité associée à la valeur z obtenue. ↩