SOMMAIRE :
Résumé
— Traduction de l'abstract
— Téléchargements
— Historique des modifications
— Notes
Résumé
En combinant les QI nationaux avec la population de chaque pays, il est possible d'estimer le QI moyen de la population mondiale : entre 85 et 87 (la page "QI moyen mondial" sur Douance avait calculé 86,62), soit environ -1σ d'écart avec la moyenne. Mais le regroupement par pays donne une distribution totalement irrégulière :
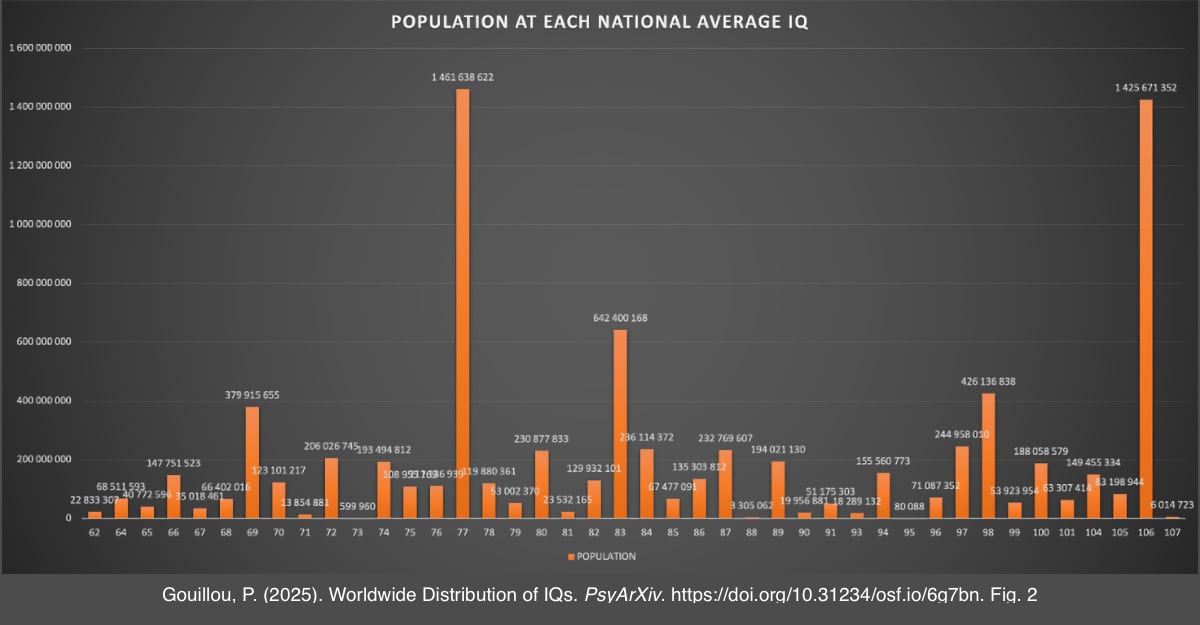
En conséquence, il est impossible de calculer directement la distribution mondiale des QI à partir de leur moyenne. Pour y parvenir, il est nécessaire de calculer indépendamment pour chaque pays les fractions de la population à chaque niveau de QI et additionner les résultats obtenus, ce qui représente des centaines de calcul.
Mais si on effectue ce calcul pour un QI de 157, on s'aperçoit que le résultat est quasiment le même que si le QI moyen mondial était de 100 ! Pourquoi ? L'explication provient de l'énorme influence de la Chine (QI=106) dans la distribution par pays qui crée un déséquilibre.
Dès lors, l'idée est de calculer, pour chaque niveau de QI, quel est ce QI moyen théorique correspondant au pourcentage de la population. Par exemple, si 2,3% est à 130 ou plus, le QI théorique moyen est de 100 (130 = +2σ). Bien sûr, à cause de la répartition inégale, il est nécessaire de refaire le calcul pour chaque niveau de QI.
Et les calculs montrent que ce QI théorique suit une progression presque (mais pas totalement) linéaire :
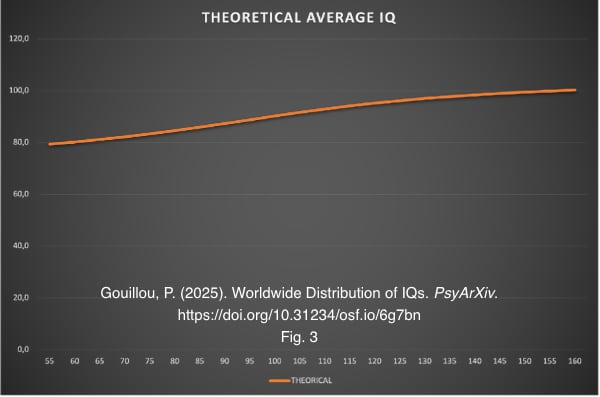
L'article publie les résultats de ces calculs pour chaque 5 points de QI entre 55 et 160. Mais il va aussi plus loin : il fournit une formule (trouvée par IA) qui permet de calculer directement ce QI théorique à partir du QI de référence pour la population mondiale. Il n'est plus besoin de faire des centaines de calculs, la formule est assez précise :
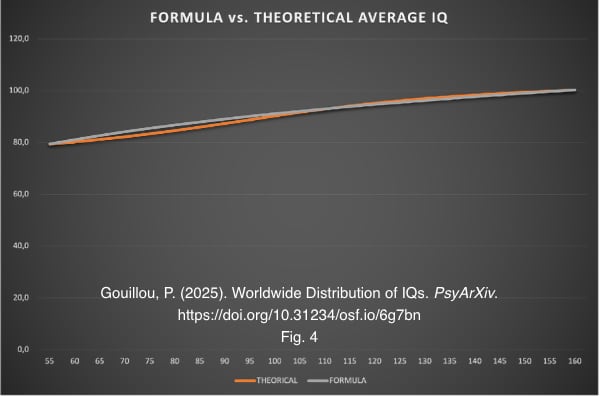
Dès lors, il est facile de calculer le nombre de personnes à chaque niveau de QI, comme le montre cette copie écran du fichier MS Excel utilisé (lien pour le télécharger ci-après) :
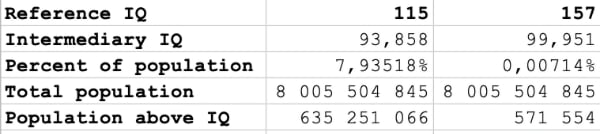
Et il est facile de calculer la distribution réelle des QI dans le monde :
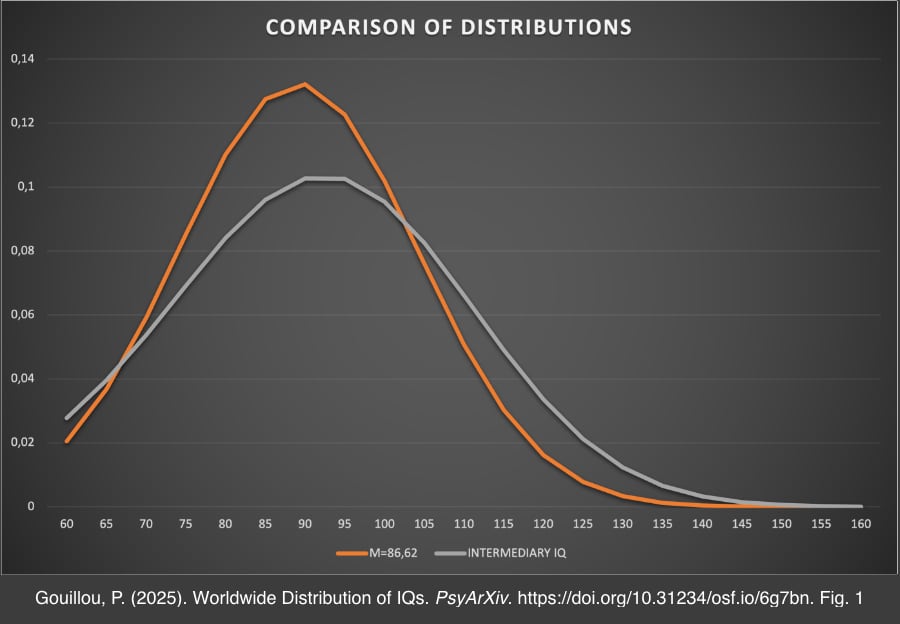
Cette image montre en orange la distribution calculée avec M=86,62, c'est-à-dire le seul calcul direct possible à partir de la moyenne mondiale, et en gris la distribution calculée selon la formule trouvée. On remarque que non seulement cette courbe n'est pas symétrique, mais aussi qu'elle est plus "aplatie" qu'une distribution normale de QI. En fait elle apparaît plus ou moins modélisable par une distribution log-normale mais la marge d'erreur est importante aussi l'article n'en parle pas.
Elle montre clairement qu'il y a plus de haut QI que la moyenne de 86,62 ne le laisse supposer.
Cette estimation a bien sûr des limites, comme l'indique l'article (p. 5-6) :
"Cette formule a des limites qu'il est important de rappeler. Premièrement, elle dépend entièrement de la validité des QI nationaux, et disproportionnellement de ceux de la Chine et de l'Inde. Deuxièmement, elle repose sur l'hypothèse que le QI est parfaitement distribué selon une loi normale avec un écart-type de 15 dans chaque pays. On sait déjà que cette deuxième hypothèse est fausse : plusieurs pays (par exemple Singapour) sont constitués de deux ou plusieurs populations dont les QI moyens sont suffisamment différents pour que leur somme ne suive pas une distribution normale parfaite. Par conséquent, cette formule doit être prise avec une marge d'erreur."1
Gouillou (2025)
Mais elle offre une meilleure estimation que ce que la simple moyenne peut fournir. Par exemple, Peter Frost s'en est servi dans son article du 2 janvier 2025 pour estimer le nombre de personnes dans le monde ayant un QI supérieur à 157 afin d'apporter des éléments quantitatifs à un débat sur X.
Traduction de l'abstract
"Les QI moyens nationaux peuvent être utilisés pour calculer un QI moyen mondial. Cependant, en raison des différences de taille des populations, ils ne sont pas distribués normalement et il est impossible de calculer la distribution du QI à partir de cette moyenne. Pour estimer le nombre de personnes dans le monde ayant un QI supérieur à une valeur donnée, il est nécessaire de passer par le calcul intermédiaire d'un QI moyen théorique suivant une distribution normale. En utilisant les données de QI moyen et de population de 204 pays, cet article fournit la formule de calcul de cet intermédiaire et donne des chiffres pour des QI allant de 55 à 160 par pas de 5 points de QI. Il montre qu'il y a beaucoup plus de QI élevés que la moyenne mondiale ne le laisse supposer. Par exemple, il y a à peu près autant de personnes dans le monde ayant un QI supérieur à 157 qu'il y en aurait si la moyenne mondiale était de 100 et si le QI était distribué selon une loi normale."2
Gouillou (2025)
Téléchargements
L'article et le fichier MS Excel de calcul sont en téléchargement libres :
Article : Gouillou, P. (2025). Worldwide Distribution of IQs. PsyArXiv, 6g7bn. doi:10.31234/osf.io/6g7bn
Fichier Excel : gouillou-2025-worldwide-distribution-of-iq-2025-01-01.xlsx
Liens
Frost, P. (2025). Reply to Elon and Sriram. Substack :Peter Frost’s Newsletter. 2 janvier 2025
Gouillou, P. (2023). QI moyen mondial. Douance. 23 Décembre 2023 - MàJ : 1er février 2024
Historique des modifications
| Date | Historique |
|---|---|
| 08 janvier 2025 | Correction faute de frappe |
| 03 janvier 2025 | 1ère Mise en ligne |
Notes
-
Traduction depuis Gouillou (2025) :
"This formula has limita1ons that are important to remember. Firstly, it is entirely dependent on the validity of national IQs, and dispropor1onately on those of China and India. Secondly, it is based on the assumption that IQ is perfectly distributed according to a Normal Law with a standard devia1on of 15 within each country. This second assumption is already known to be false: several countries (e.g. Singapore) are made up of two or more popula1ons with average IQs that are sufficiently different that their sum does not follow a perfect normal distribu1on. Consequently, this formula should be taken with a margin of error."
-
Traduction depuis Gouillou (2025) :
"National average IQs can be used to calculate a global average IQ. However, due to differences in population sizes, they are not normally distributed, and it is impossible to calculate the IQ distribution from this average. To estimate the number of people in the world with an IQ above a given value, it is necessary to go through the intermediate calculation of a theoretical average IQ following a Normal Distribution. Using the average IQ and population data of 204 countries, this article provides the formula for calculating this intermediate and gives figures for IQs from 55 to 160 in steps of 5 IQ points. It shows that there are many more high IQs than the world average would suggest. For example, there are about as many people in the world with an IQ above 157 as there would be if the world average were 100 and IQ were distributed according to a normal distribution."